Discrete Signal Processing Fourier Transform Cheat Note
Table of Contents
1. Fourier series coefficients for Continuous signal #
Asking deriving coefficients comes with periodic signal.: \(x(t) \rightarrow a_k\)
1.1 (CT FS) Basic concept of continuous Fourier coefficients #
$$ \begin{gathered} x(t): \text { Periodic signal } \ T: \text { Fundamental Period } \ \end{gathered} $$
$$ \begin{gathered} \omega_0=\frac{2 \pi}{T} \quad & \quad f_0=\frac{1}{T}(\text { freq }) \ \end{gathered} $$
$$ \begin{gathered} \quad x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{j k \omega_0 t}=\sum_{k=-\infty}^{+\infty} a_k e^{j k(2 \pi / T) t} \end{gathered} $$
1.2 (CT FS) Continuous-Time, Fourier Series #
Convert periodic signal to fourier coefficients : \(x(t) \stackrel{F S}{\rightarrow} a_k\)
$$ \begin{gathered} a_k=\frac{1}{T} \int _T x(t) e^{-j k \omega_0 t} d t \ \end{gathered} $$
$$ or $$
$$ \begin{gathered} a_k=\frac{1}{T} \int_T x(t) e^{-j k(2 \pi / T) t} d t \end{gathered} $$
1.3 (CT IFS) Continuous-Time, Inverse Fourier Series #
Fourier coefficients to peridoic signal : \(a_k \stackrel{I F S}{\longrightarrow} x(t)\)
$$ x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{j k \omega_0 t}=\sum_{k=-\infty}^{+\infty} a_k e^{j k(2 \pi / T) t} $$
1.4 Properties of Continuous-Time Fourier Series #
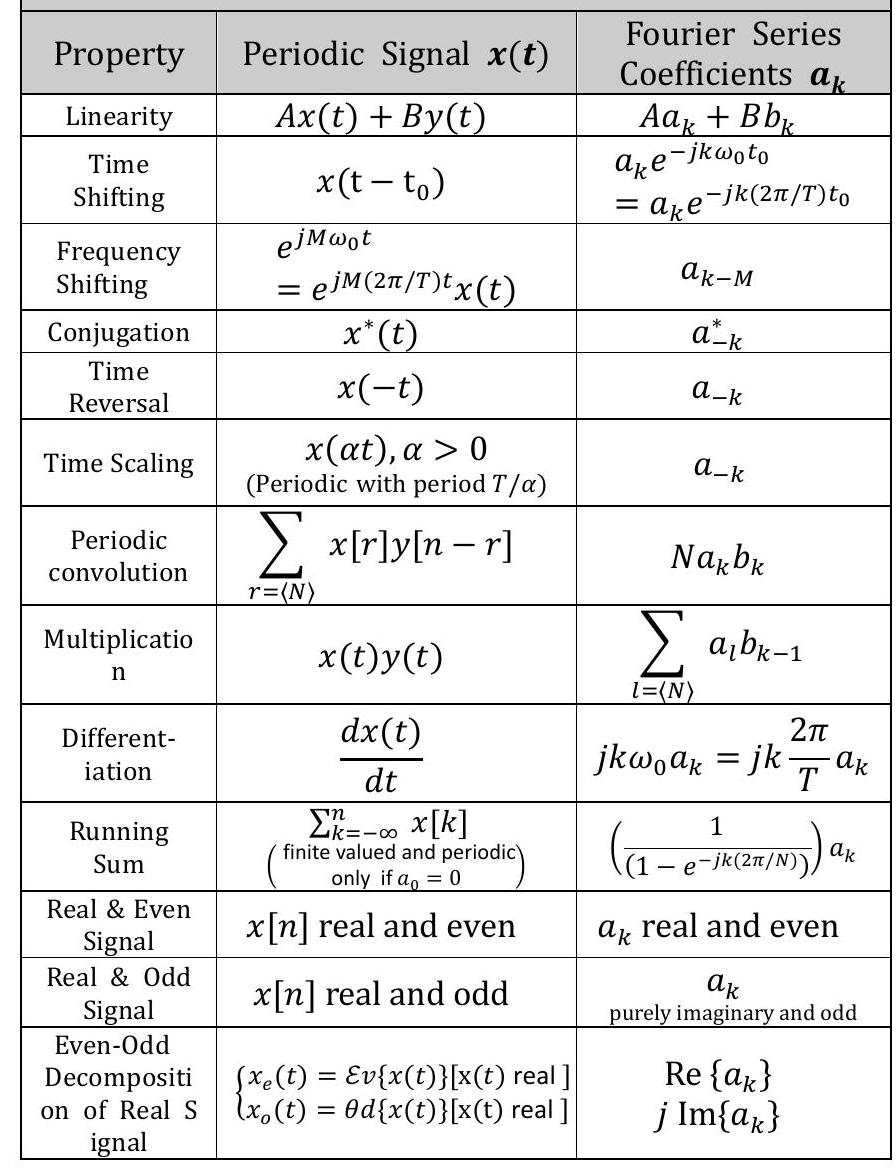
2. Fourier coefficients for Discrete signal #
$$ \begin{gathered} x[n] \rightarrow \boldsymbol{a}_{\boldsymbol{k}} \end{gathered} $$ Asking deriving coefficients comes with periodic signal.
2.1 (DT FS) Basic concept of discrete Fourier coefficients \(x[n]: Periodic\) #
$$ \begin{gathered} x[n]: \text { Periodic signal } \end{gathered} $$
$$ N \text { : Fundamental Period (LCM of } 2 \pi \text { ) } $$
$$ \begin{gathered} \omega_0=\frac{2 \pi}{N} \quad & \quad f_0=\frac{1}{T}(\text { freq }) \end{gathered} $$
$$ x[n]=\sum_{k=\langle N\rangle} a_k e^{j k \omega_0 n}=\sum_{k=\langle N\rangle} a_k e^{j k(2 \pi / N) n} $$
2.3 (DT FS) Discrete-Time, Fourier Series #
$$\begin{gathered} a_{k}=\frac{1}{N} \sum_{n=\langle N\rangle} x[n] e^{-j k \omega_{0} n} \ a_{k}=\frac{1}{N} \sum_{n=\langle N\rangle} x[n] e^{-j k(2 \pi / N) n} \end{gathered}$$
$$\begin{aligned} & x[n] \stackrel{F S}{\rightarrow} a_{k} \end{aligned}$$
2.4 (DT IFS) Discrete-Time, Inverse Fourier Series #
$$a_{k} \stackrel{I F S}{\rightarrow} x[n] \quad x[n]=\sum_{k=\langle N\rangle} a_{k} e^{j k \omega_{0} n}=\sum_{k=\langle N\rangle} a_{k} e^{j k(2 \pi / N) n}$$
2.5 Properties of Continuous-Time Fourier Series #
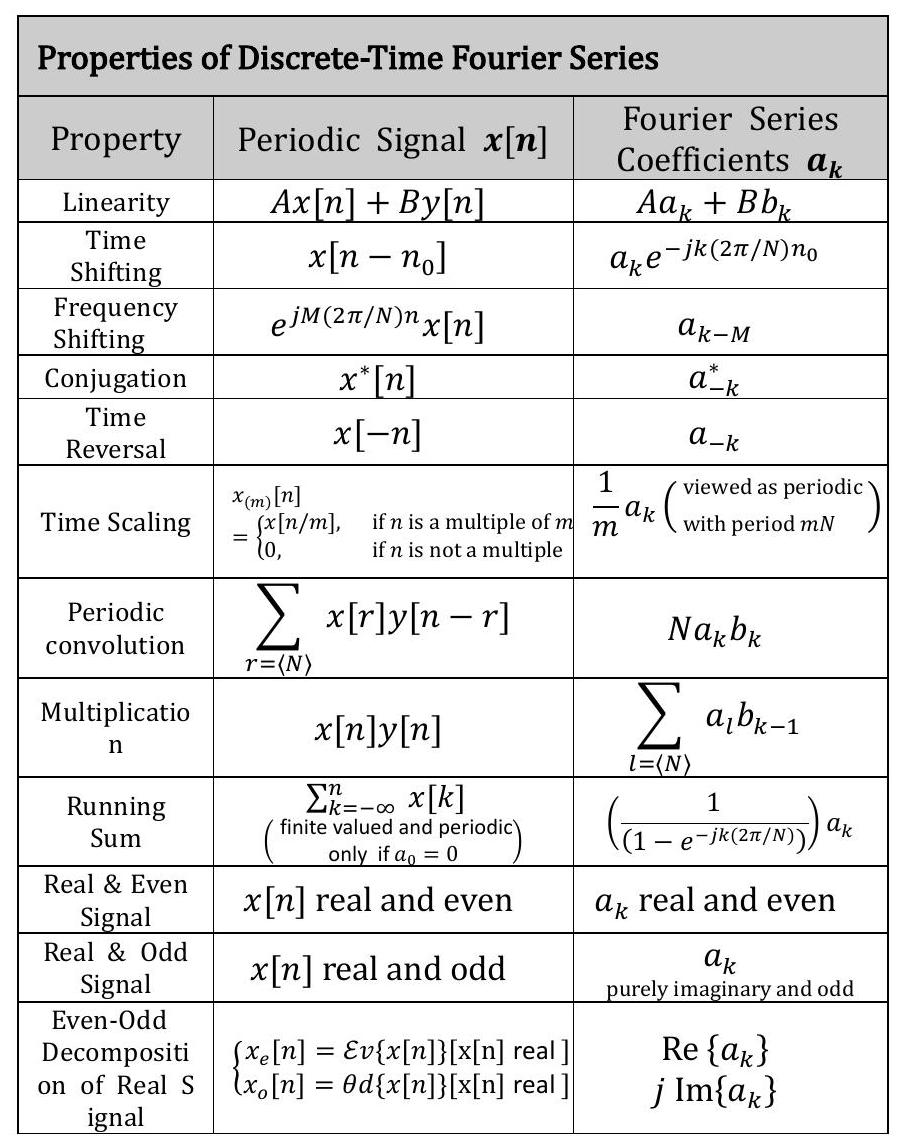
3 Fourier transform for Continuous-time signal \(x(t)\) : #
3.1 (CT FT) Continuous-Time, Fourier Transform ( periodic) #
$$ x(t) \stackrel{F T}{\longrightarrow} X(j \omega) $$
$$ \tilde{x}(t): \text { single sliced periodic sig } \ $$
$$ a_k=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \tilde{x}(t) e^{-j k \omega_0 t} d t $$ $$ X(j \omega)=T a_k $$
3.2 (CT FT) Continuous-Time, Fourier Transform (aperiodic) #
$$x(t) \stackrel{F T}{\rightarrow} X(j \omega) \quad X(j \omega)=\int_{-\infty}^{+\infty} x(t) e^{-j \omega t} d t$$
3.3 (CT IFT) Continuous-Time, Inverse Fourier Transform #
$$X(j w) \stackrel{I F T}{\rightarrow} x(t) \quad x(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} X(j \omega) e^{j \omega t} d \omega$$
3.4 Properties of Continuous Fourier Transform #

3.5 Basic Continuous Fourier Transform Pairs #

4 Fourier transform for Discrete-time signal \(x[n]\) #
Most of case, aperiodic signals comes…
4.1 (DT FT) Discrete-Time, Fourier Transform #
$$x[n] \stackrel{F T}{\rightarrow} X\left(e^{j \omega}\right) \quad X\left(e^{j \omega}\right)=\sum_{n=-\infty}^{+\infty} x[n] e^{-j \omega n}$$
4.2 (DT IFT) Discrete-Time, Inverse Fourier Transform #
$$X\left(e^{j \omega}\right) \stackrel{I F T}{\rightarrow} x[n] \quad x[n]=\frac{1}{2 \pi} \int_{2 \pi} X\left(e^{j \omega}\right) e^{j \omega n} d \omega$$
4.3 Properties of Discrete Fourier Transform #

4.4 Basic Discrete Fourier Transform Pairs #


