1. 연속 신호의 푸리에 급수 계수#
계수 유도 문제는 주기 신호와 함께 출제됩니다.: \(x(t) \rightarrow a_k\)
1.1 (CT FS) 연속 푸리에 계수의 기본 개념#
$$ \begin{gathered} x(t): \text { Periodic signal } \ T: \text { Fundamental Period } \ \end{gathered} $$
$$ \begin{gathered} \omega_0=\frac{2 \pi}{T} \quad & \quad f_0=\frac{1}{T}(\text { freq }) \ \end{gathered} $$
$$ \begin{gathered} \quad x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{j k \omega_0 t}=\sum_{k=-\infty}^{+\infty} a_k e^{j k(2 \pi / T) t} \end{gathered} $$
1.2 (CT FS) 연속시간 푸리에 급수#
주기 신호를 푸리에 계수로 변환 : \(x(t) \stackrel{F S}{\rightarrow} a_k\)
$$ \begin{gathered} a_k=\frac{1}{T} \int _T x(t) e^{-j k \omega_0 t} d t \ \end{gathered} $$
$$ or $$
$$ \begin{gathered} a_k=\frac{1}{T} \int_T x(t) e^{-j k(2 \pi / T) t} d t \end{gathered} $$
1.3 (CT IFS) 연속시간 역 푸리에 급수#
푸리에 계수를 주기 신호로 변환 : \(a_k \stackrel{I F S}{\longrightarrow} x(t)\)
$$ x(t)=\sum_{k=-\infty}^{+\infty} a_k e^{j k \omega_0 t}=\sum_{k=-\infty}^{+\infty} a_k e^{j k(2 \pi / T) t} $$
1.4 연속시간 푸리에 급수의 성질#
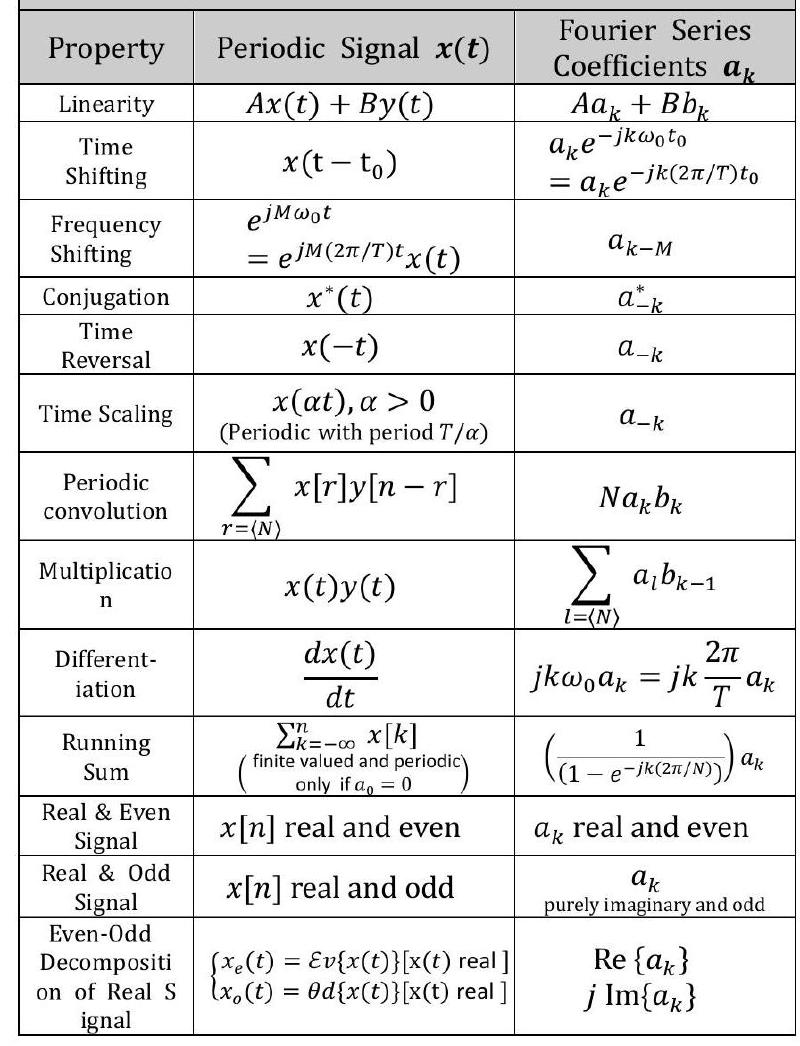
2. 이산 신호의 푸리에 계수#
$$ \begin{gathered} x[n] \rightarrow \boldsymbol{a}_{\boldsymbol{k}} \end{gathered} $$ 계수 유도 문제는 주기 신호와 함께 출제됩니다.
2.1 (DT FS) 이산 푸리에 계수의 기본 개념 \(x[n]: Periodic\)#
$$ \begin{gathered} x[n]: \text { Periodic signal } \end{gathered} $$
$$ N \text { : Fundamental Period (LCM of } 2 \pi \text { ) } $$
$$ \begin{gathered} \omega_0=\frac{2 \pi}{N} \quad & \quad f_0=\frac{1}{T}(\text { freq }) \end{gathered} $$
$$ x[n]=\sum_{k=\langle N\rangle} a_k e^{j k \omega_0 n}=\sum_{k=\langle N\rangle} a_k e^{j k(2 \pi / N) n} $$
2.3 (DT FS) 이산시간 푸리에 급수#
$$\begin{gathered} a_{k}=\frac{1}{N} \sum_{n=\langle N\rangle} x[n] e^{-j k \omega_{0} n} \ a_{k}=\frac{1}{N} \sum_{n=\langle N\rangle} x[n] e^{-j k(2 \pi / N) n} \end{gathered}$$
$$\begin{aligned} & x[n] \stackrel{F S}{\rightarrow} a_{k} \end{aligned}$$
2.4 (DT IFS) 이산시간 역 푸리에 급수#
$$a_{k} \stackrel{I F S}{\rightarrow} x[n] \quad x[n]=\sum_{k=\langle N\rangle} a_{k} e^{j k \omega_{0} n}=\sum_{k=\langle N\rangle} a_{k} e^{j k(2 \pi / N) n}$$
2.5 연속시간 푸리에 급수의 성질#
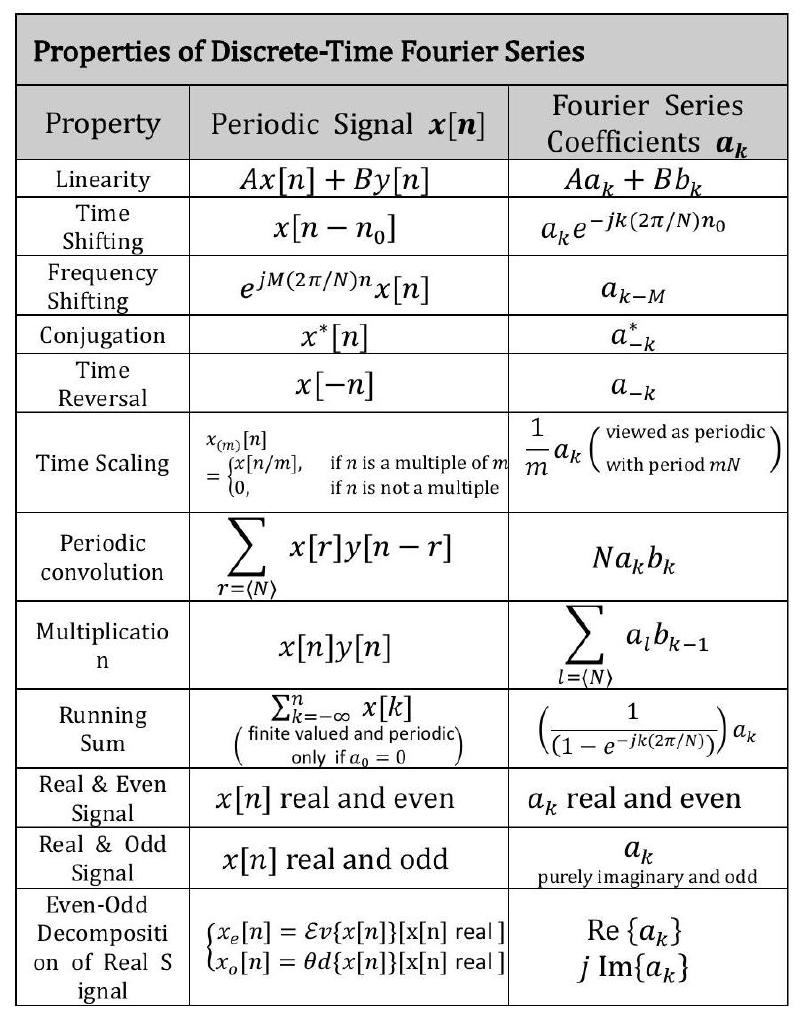
3 연속시간 신호 \(x(t)\)의 푸리에 변환 :#
3.1 (CT FT) 연속시간 푸리에 변환 (주기)#
$$ x(t) \stackrel{F T}{\longrightarrow} X(j \omega) $$
$$ \tilde{x}(t): \text { single sliced periodic sig } \ $$
$$ a_k=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} \tilde{x}(t) e^{-j k \omega_0 t} d t $$ $$ X(j \omega)=T a_k $$
3.2 (CT FT) 연속시간 푸리에 변환 (비주기)#
$$x(t) \stackrel{F T}{\rightarrow} X(j \omega) \quad X(j \omega)=\int_{-\infty}^{+\infty} x(t) e^{-j \omega t} d t$$
3.3 (CT IFT) 연속시간 역 푸리에 변환#
$$X(j w) \stackrel{I F T}{\rightarrow} x(t) \quad x(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} X(j \omega) e^{j \omega t} d \omega$$
3.4 연속 푸리에 변환의 성질#

3.5 기본 연속 푸리에 변환 쌍#

4 이산시간 신호 \(x[n]\)의 푸리에 변환#
대부분의 경우 비주기 신호가 출제됩니다…
4.1 (DT FT) 이산시간 푸리에 변환#
$$x[n] \stackrel{F T}{\rightarrow} X\left(e^{j \omega}\right) \quad X\left(e^{j \omega}\right)=\sum_{n=-\infty}^{+\infty} x[n] e^{-j \omega n}$$
4.2 (DT IFT) 이산시간 역 푸리에 변환#
$$X\left(e^{j \omega}\right) \stackrel{I F T}{\rightarrow} x[n] \quad x[n]=\frac{1}{2 \pi} \int_{2 \pi} X\left(e^{j \omega}\right) e^{j \omega n} d \omega$$
4.3 이산 푸리에 변환의 성질#

4.4 기본 이산 푸리에 변환 쌍#

